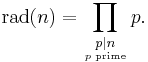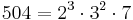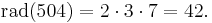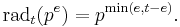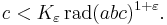Radical of an integer

In number theory, the radical of a positive integer n is defined as the product of the prime numbers dividing n:

$\displaystyle\mathrm{rad}(n)=\prod_{\scriptstyle p\mid n\atop p\text{ prime}}p.\,$

Examples

Radical numbers for the first few positive integers are

1, 2, 3, 2, 5, 6, 7, 2, 3, 10, ... (sequence A007947 in OEIS).

For example,

$504=2^3\cdot3^2\cdot7$

and therefore

$\mathrm{rad}(504)=2\cdot3\cdot7=42.\,$

Properties

The function 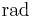$\mathrm{rad}$ is multiplicative (but not completely multiplicative).

The radical of any integer n is the largest square-free divisor of n, and so also described as the square-free kernel of n. The definition is generalized to the largest t-free divisor of n, 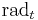$\mathrm{rad}_t$ , which are multiplicative functions which act on prime powers as

$\mathrm{rad}_t(p^e) =p^{\mathrm{min}(e,t-e)}.$

The cases t=3 and t=4 are tabulated in A007948 and A058035.

One of the most striking applications of the notion of radical occurs in the abc conjecture, which states that, for any ε > 0, there exists a finite K_ε such that, for all triples of coprime positive integers a, b, and c satisfying a + b = c,

$c < K_\varepsilon\, \operatorname{rad}(abc)^{1%2B\varepsilon}.$

Furthermore, it can be shown that the nilpotent elements of 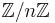$\mathbb{Z}/n\mathbb{Z}$ are all of the multiples of rad(n).

References

Guy, Richard K. (2004). Unsolved Problems in Number Theory. Springer-Verlag. p. 102. ISBN 0-387-20860-7.